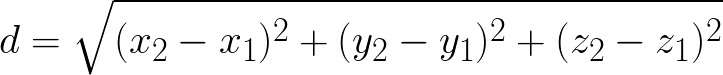The Python Shell
In this module you can learn:
- How to use Python as a pocket calculator
- How to store data in variables
- How to import functions from Python modules
Traces in the desert sand…

Python can be used as a calculator:
>>> 1+2
>>> 3
Fill in dashed lines with appropriate values using the python interactive shell
>>> 1 _ _ 2
>>> 3
>>> 12 - _ _
4
>>> _ _ * 5
20
>>> _ _ ** 2
81
Python can be used to store variables:
>>> camels = 9
>>> camels
_ _
>>> silk = camels * _ _
>> silk
36
>>> math.sqrt(silk)
_ _
>>> math.pow(camels, _ _ )
81.0
The interactive Python shell
You can access the shell by typing python in a command-line terminal
$ python
Python 2.7.9 (default, Apr 2 2015, 15:33:21)
[GCC 4.9.2] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>>
You can leave the shell with Ctrl-D
Challenge #1
Open a Python interactive session (the Python shell):
- Calculate the sum and difference of two numbers
- Divide two numbers. Try 5/3.
- Then try 5.0/3
- Calculate 3x5
- Calculate a power of 2
Variables
Variables are containers for data.
Variable names may be composed of letters, underscores and, after the first position, also digits.
>>> camels = 9
>>> camels
9
>>> silk = camels * 4
>> silk
36
The math module
Sometimes you need more complex mathematical constants and functions
- square root
- factorial
- sine or cosine
- pi
- log
Python groups them together in a text file. You can access them by importing the file.
import math
Find the matching pairs of functions and x/y values.

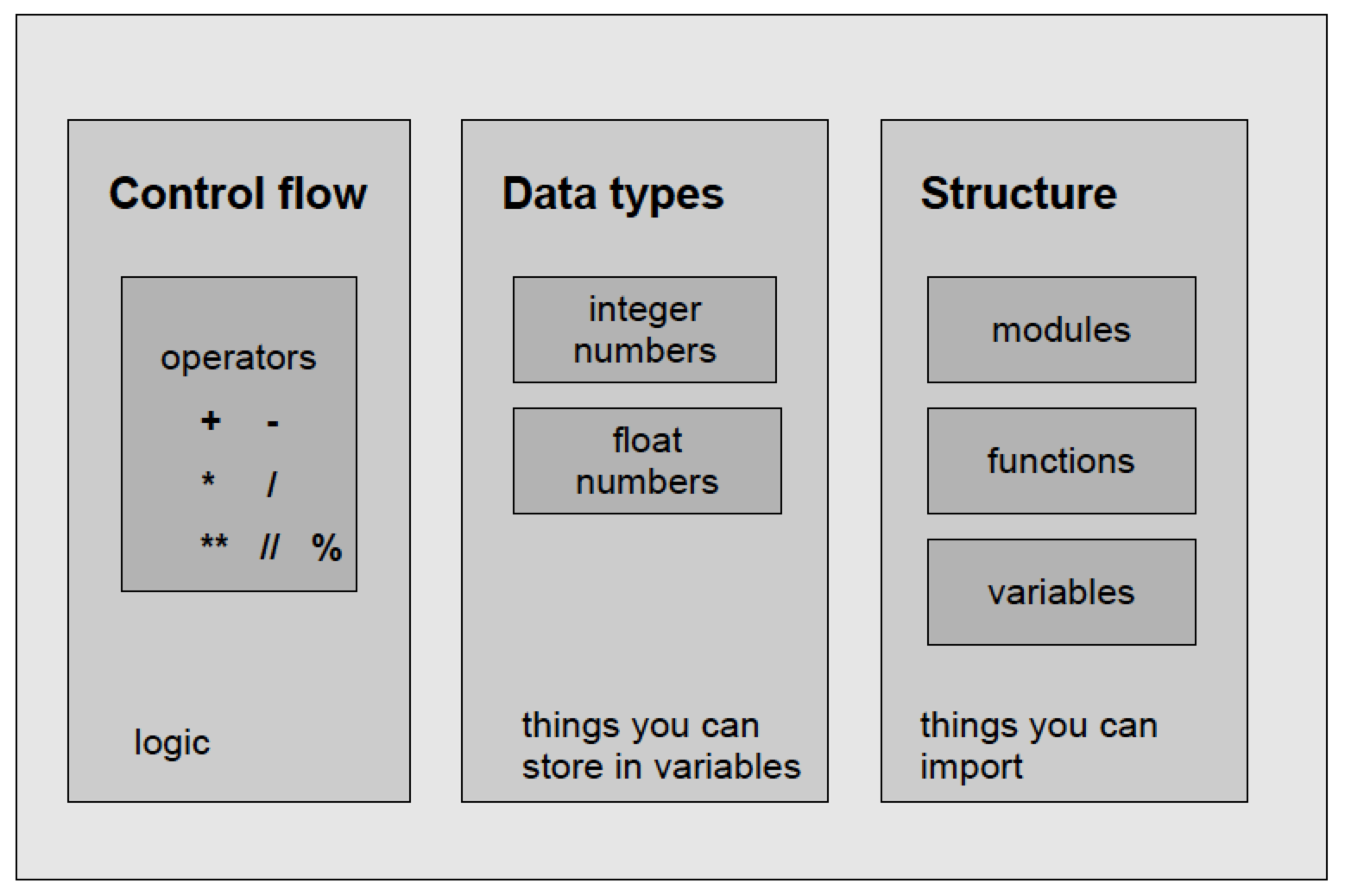
Components of Python
The Dogma of Programming
- First, make it work.
- Second, make it nice.
- Third, and only if it is really necessary, make it fast.
Challenge #2
- The diameter of a cell is 10 μm.
- What volume does that cell have given it is a perfect sphere?
- Use Python to do the calculation.
- Use variables for the parameters.
- Print the volume to the screen
See the Solution to challenge #2
Challenge #3
Calculate the distance between two points in the 3D space
Given two points in the Cartesian space:
P1 = (43.64, 30.72, 88.95) P2 = (45.83, 31.11, 92.04)
- Use Python to calculate their distance
- Use variables for the parameters
- Print the distance to the screen
The formula for calculating the distance is:
See the Solution to challenge #3
Challenge #4
Find cysteine bonds in the Insulin structure
- Data in 2OMH.pdb
- Lines containing ‘SG’
- x, y, z coordinates
- Use what you learnt from Task 2
HEADER HORMONE 22-JAN-07 2OMH
TITLE STRUCTURE OF HUMAN INSULIN COCRYSTALLIZED WITH ARG-12 PEPTIDE IN
TITLE 2 PRESENCE OF UREA
COMPND MOL_ID: 1;
COMPND 2 MOLECULE: INSULIN A CHAIN;
COMPND 3 CHAIN: A
COMPND 4 MOL_ID: 2;
COMPND 5 MOLECULE: INSULIN B CHAIN;
COMPND 6 CHAIN: B
ATOM 1 N GLY A 1 -11.626 14.280 1.013 1.00 19.13 N
ATOM 2 CA GLY A 1 -12.164 13.430 2.116 1.00 18.24 C
ATOM 3 C GLY A 1 -11.587 13.815 3.470 1.00 17.90 C
ATOM 4 O GLY A 1 -10.907 14.833 3.590 1.00 18.08 O
ATOM 5 N ILE A 2 -11.836 12.995 4.484 1.00 17.57 N
ATOM 6 CA ILE A 2 -11.397 13.317 5.832 1.00 17.78 C
ATOM 7 C ILE A 2 -9.875 13.489 5.951 1.00 17.93 C
ATOM 8 O ILE A 2 -9.408 14.371 6.670 1.00 17.80 O
ATOM 9 CB ILE A 2 -11.922 12.289 6.869 1.00 17.86 C
ATOM 10 CG1 ILE A 2 -11.767 12.855 8.281 1.00 17.66 C
ATOM 11 CG2 ILE A 2 -11.242 10.918 6.680 1.00 18.86 C
ATOM 12 CD1 ILE A 2 -12.434 12.031 9.365 1.00 19.10 C
ATOM 13 N VAL A 3 -9.110 12.680 5.224 1.00 18.04 N
ATOM 14 CA VAL A 3 -7.652 12.759 5.315 1.00 19.40 C
ATOM 15 C VAL A 3 -7.193 14.102 4.747 1.00 19.43 C
ATOM 16 O VAL A 3 -6.395 14.820 5.357 1.00 19.23 O
Challenge #5
The hydrolysis of one phosphodiester bond from ATP results in a standard Gibbs energy (ΔG0) of -30.5 kJ/mol. According to biochemistry textbooks, the real ΔG value depends on the concentration of the compounds and these concentrations can differ quite a lot among tissues.
The Gibbs energy as a function of the concentrations of the compounds can be written as:
ΔG = ΔG0 + RT * ln ( [ADP] * [Pi] / [ATP])
Knowing that:
R = 0.00831
T = 298
- Use Python to calculate the real DG in the tissues reported in the table.
- Use variables for the parameters.
- Print the results to the screen.
See See the Solution to challenge #5
Recap
- You can use the Python shell as a pocket calculator.
- Variables are containers for data.
- Modules are containers for data and functions
- You can leave the shell by Ctrl-D.
Back
Back to main page.