5. Statistical Inference: Two-sample t-test

1 Smelly armpit example

• Smelly armpits are not caused by sweat, itself. The smell is caused by specific micro-organisms belonging to the group of Corynebacterium spp. that metabolise sweat. Another group of abundant bacteria are the Staphylococcus spp., these bacteria do not metabolise sweat in smelly compounds.

• The CMET-group at Ghent University does research to on transplanting the armpit microbiome to save people with smelly armpits.

• Proposed Therapy:

  1. Remove armpit-microbiome with antibiotics
  2. Influence armpit microbiome with microbial transplant (https://youtu.be/9RIFyqLXdVw)

• Experiment:

  • 20 subjects with smelly armpits are attributed to one of two treatment groups
  • placebo (only antibiotics)
  • transplant (antibiotica followed by microbial transplant).
  • The microbiome is sampled 6 weeks upon the treatment
  • The relative abundance of Staphylococcus spp. on Corynebacterium spp. + Staphylococcus spp. in the microbiome is measured via DGGE (Denaturing Gradient Gel Electrophoresis).

---

1.1 Import the data

ap <- read_csv("https://raw.githubusercontent.com/GTPB/PSLS20/master/data/armpit.csv")
ap

1.2 Data exploration

We plot the direct relative abundances in function of the treatment group. With the ggplot2 library we can easily build plots by adding layers.

ap %>% ggplot(aes(x = trt, y = rel)) +
  geom_boxplot(outlier.shape = NA) +
  geom_point(position = "jitter")

ap %>% ggplot(aes(sample = rel)) +
  geom_qq() +
  geom_qq_line() +
  facet_wrap(~trt)

---

2 Two sample T-test

2.1 Notation

Suppose that \(Y_{ij}\) is the response for subjects \(i=1,\ldots, n_j\) from population \(j=1,2\).

Use of the term treatment or group instead of population

Here the treatment is \(j=1\) microbial transplant vs \(j=2\) placebo.

We assume

\[Y_{ij}\text{ i.i.d. } N(\mu_j,\sigma^2)\;\;\;i=1,\ldots,n_i\;j=1,2.\]

Note, that we assume equal variances homoscedastic

(Unequal variances are referred to as heteroscedastic)

---

2.2 Hypotheses

Test \[ H_0: \mu_1 = \mu_2 \] against \[ H_1: \mu_1 \neq \mu_2 .\]

\(H_1\) is again the research hypothesis: the average relative abundance of Staphylococcus spp. is different upon microbial transplant then upon placebo treatment.

\(H_0\) and \(H_1\) can also be specified in terms of the effect size between the two treatments, \(\mu_1-\mu_2\) \[H_0: \mu_1-\mu_2 = 0,\] \[H_1: \mu_1-\mu_2 \neq 0.\]

We can estimate the effect size using the difference in sample means: \[\hat \mu_1-\hat \mu_2=\bar Y_1 -\bar Y_2.\]

---

2.3 Variance estimator

The experimental units are independent so the sample means are also independent and the variance on the difference is \[\text{Var}_{\bar Y_1 -\bar Y_2}=\frac{\sigma^2}{n_1}+\frac{\sigma^2}{n_2}=\sigma^2 \left(\frac{1}{n_1}+\frac{1}{n_2}\right).\]

And the standard error becomes \[\sigma_{\bar Y_1 -\bar Y_2}=\sigma\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}.\]

The variance can be estimated within each group using the sample variance:

\[S_1^2 = \frac{1}{n_1-1}\sum_{i=1}^{n_1} (Y_{i1}-\bar{Y}_1)^2.\]

\[S_2^2 = \frac{1}{n_2-1}\sum_{i=1}^{n_2} (Y_{i2}-\bar{Y}_2)^2.\]

But, if we assume equal variances \(\sigma_1^2=\sigma_2^2=\sigma^2\) than we can estimate the variance more precise by using all observations in both groups. This variance estimator is also referred to as the pooled variance estimator: \(S^2_p\).

So \(S_1^2\) en \(S_2^2\) are estimators of the same parameter \(\sigma^2\).

And we can combine them into one estimator based on all \(n_1+n_2\) observations:

\[ S_p^2 = \frac{n_1-1}{n_1+n_2-2} S_1^2 + \frac{n_2-1}{n_1+n_2-2} S_2^2 = \frac{1}{n_1+n_2-2}\sum_{j=1}^2\sum_{i=1}^{n_j} (Y_{ij} - \bar{Y}_j)^2.\]

\[ S_p^2= \sum\limits_{j=1}^2\sum\limits_{i=1}^{n_j} \frac{(Y_{ij}-\bar{Y}_{.j})^2}{n_1+n_2-2}\]

The pooled variance estimator uses the squared deviations of the observations from their group mean and has \(n_1+n_2-2\) degrees of freedom.

---

2.4 Test statistic

Two-sample \(t\)-teststatistiek:

\[T = \frac{\bar{Y}_1-\bar{Y}_2}{\sqrt{\frac{S_p^2}{n_1}+\frac{S_p^2}{n_2}}} = \frac{\bar{Y}_1 - \bar{Y}_2}{S_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}.\]

The statistic T follows a t-distribution with \(n_1+n_2-2\) under \(H_0\) is all data are independent, normally distributed and have equal variances.

---

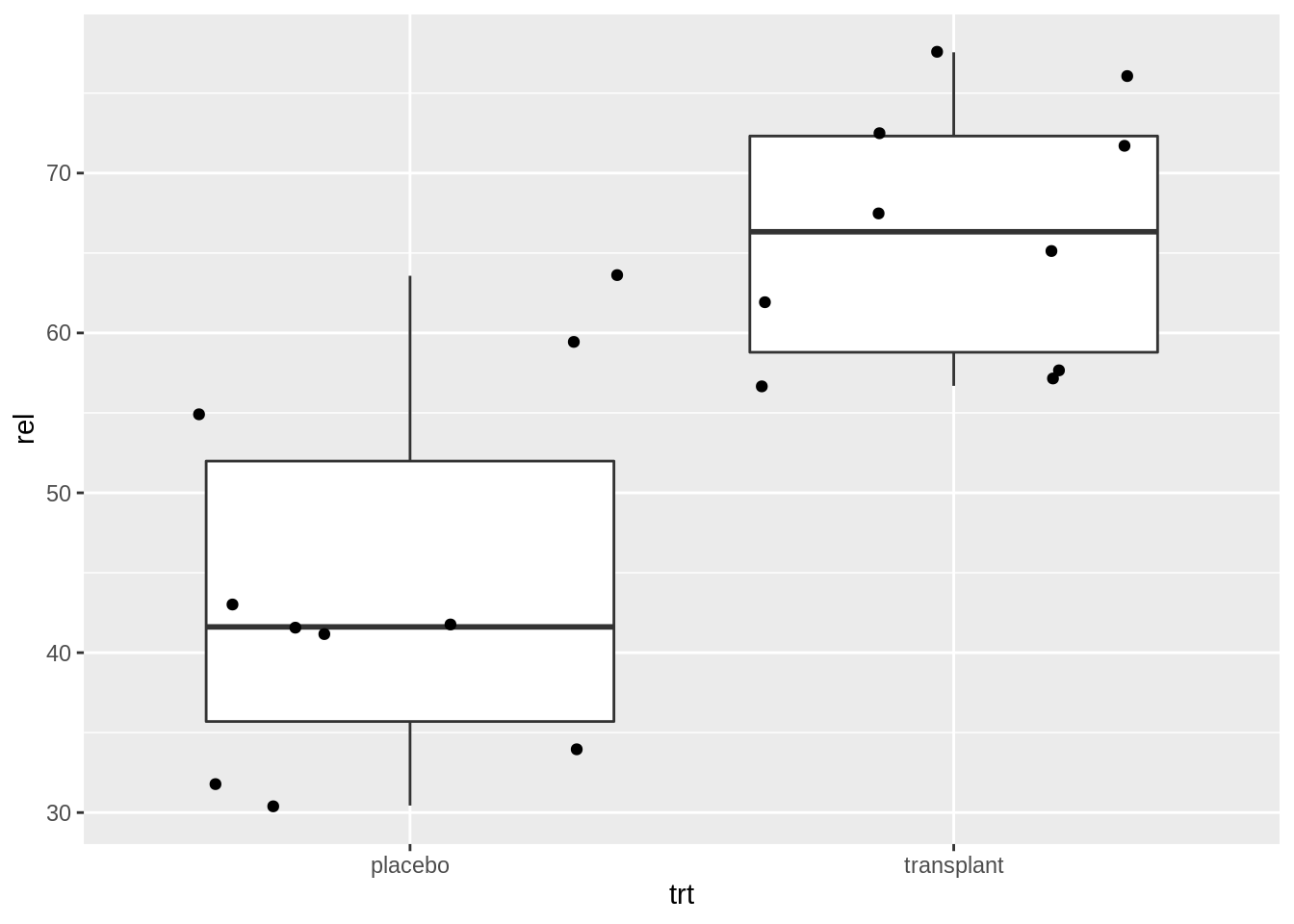
2.5 Armpit example

We can implement the test in R:

t.test(rel ~ trt, data = ap, var.equal = TRUE)

    Two Sample t-test

data:  rel by trt
t = -5.0334, df = 18, p-value = 8.638e-05
alternative hypothesis: true difference in means between group placebo and group transplant is not equal to 0
95 percent confidence interval:
 -31.53191 -12.96072
sample estimates:
   mean in group placebo mean in group transplant 
                44.15496                 66.40127 

On the \(5\%\) significance level we reject the null hypothesis in favor of the alternative hypothesis and conclude that the relative abundance of Staphylococcus spp. is on average extreme significant larger is in transplantation group than in the placebo group.

If there is no effect of the transplant we have a probability of less then 9 in \(100000\) to observe a test statistic in a random sample that is at least as extreme as what we observed in the armpit experiment.

This is extremely rare under \(H_0\).

If \(H_1\) is correct, we expect that the test statistic is larger in absolute value and expect small p-values. Hence we decide that there is a lot of evidence against \(H_0\) in favour of \(H_1\).

Good statistical practice is to report the \(p\)-value, but also effect size along with its confidence interval. So that we can judge the statistical significance and the biological relevance.

2.5.1 Conclusion

On average the relative abundance of Staphylococcus spp. in the microbiome of the armpit in the transplant group is extremely significantly different from that in the placebo group (\(p<<0.001\)). The relative abundance of Staphylococcus spp. is on average 22.2% larger in the transplant group than in the placebo group (95% CI [13.0,31.5]%).

---

3 Assumptions

Validity of t-test depends on distributional assumptions:

• Independence (design)
• One-sample t-test: normality of the observations
• Paired t-test: normality of the difference
• Two-sample t-test: Normality of the observations in both groups, and equal variances.

If the assumptions are not met, the null distribution does not follow a t-distribution, and, the p-values and critical values are incorrect.

To construct confidence intervals we also rely on these assumptions.

• We used quantiles from the t-distribution to calculate the lower and upper limit.

• The correct coverage of the CI depends on these assumptions

---

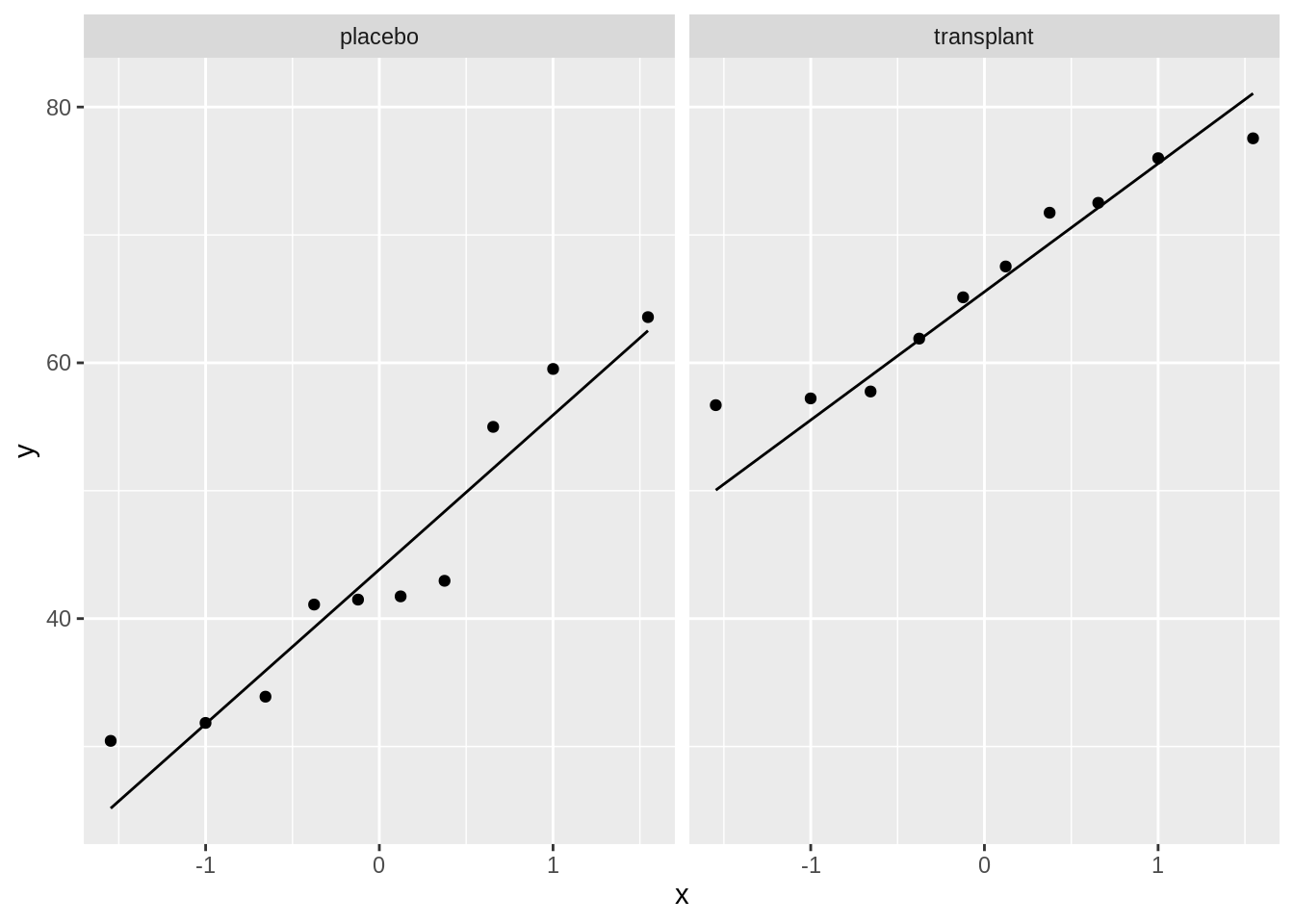
3.1 Evaluate normality

• Boxplots and histograms: shape of distribution and outliers

• QQ-plots

There also exist hypothesis tests (goodness-of-fit test), but their null hypothesis is that the data are normally distributed so we make a weak conclusion!

• Kolmogorov-Smirnov, Shapiro-Wilk en Anderson-Darling.
• In small samples they have a low power
• In large samples they often flag very small deviations as significant

Recommendation

• Start with graphical exploration of the data and keep the sample size in mind to avoid overinterpretation of the plots.

• If you have doubts, use simulation where you simulate data with the same sample size from a Normal distribution with the same mean and variance as the one that you observed in the sample

• If you observed deviations of normality check in the literature how sensitive your method is such deviations of normality. (e.g. T-tests for instance are rather insensitive to deviations as long as the distribution of the data is symmetric.)

• In large samples you can resort to the central limit theorem.

• You might resort to transformations of the response.

---

3.2 Homoscedasticity

• Boxplots: The box size is the inter quartile range (IQR) a robust estimator of the variance.

• If the differences are not large \(\rightarrow\) homoscedasticiteit

• Again you can use simulation to get insight in the differences you can expect.

• Formal F-test can be used to compare the variances, but again under the null you assume equal variances, so the same criticism as for normality tests applies here.

---

3.3 Welch modified t-test

If the data are heteroscedastic, you can use a Welch two-sample T-test, which no longer uses the pooled variance estimator.

\[T = \frac{\bar{Y}_1 - \bar{Y}_2}{\sqrt{\frac{S^2_1}{n_1}+\frac{S^2_2}{n_2}}}\] with \(S^2_1\) en \(S^2_2\) the sample variances in both groups.

This statistic follows approximately a t-distribution with a number of degrees of freedom between \(\text{min}(n_1-1,n_2-1)\) and \(n_1+n_2-2\).

In R the degrees of freedom are estimated using the Welch- Satterthwaite approximation. You can do this by using the t.test function with argument var.equal=FALSE.

t.test(rel ~ trt, data = ap, var.equal = FALSE)

    Welch Two Sample t-test

data:  rel by trt
t = -5.0334, df = 15.892, p-value = 0.0001249
alternative hypothesis: true difference in means between group placebo and group transplant is not equal to 0
95 percent confidence interval:
 -31.62100 -12.87163
sample estimates:
   mean in group placebo mean in group transplant 
                44.15496                 66.40127 

Note that you can see that the Welch T-test is adopted in the title. The adjusted degrees of freedom are \(df = 17.876\) \(\pm\) to that of the conventional T-test, because the variances are approximately equal.

---

4 How to report?

• In the scientific literature there is too much attention for p-values

• It is much more informative to combine an estimate with its confidence interval.

Rule of thumb:

Report an estimate together with its confidence interval (and its p-value)

1. The result of the test can be derived of the confidence interval
2. It allows the reader to judge scientific relevance.

t.test(rel ~ trt, data = ap)

    Welch Two Sample t-test

data:  rel by trt
t = -5.0334, df = 15.892, p-value = 0.0001249
alternative hypothesis: true difference in means between group placebo and group transplant is not equal to 0
95 percent confidence interval:
 -31.62100 -12.87163
sample estimates:
   mean in group placebo mean in group transplant 
                44.15496                 66.40127 

The result of an \(\alpha\)-level t-test is equivalent with comparing the effect size under \(H_0\) with the \(1-\alpha\) CI.

An effect can be extremely statistically significant, but scientifically irrelevant. With a CI you will spot this.

---

This work is licensed under the CC BY-NC-SA 4.0 licence.