Exercise 7.2: ANOVA on the cuckoo dataset - solution
Lieven Clement, Jeroen Gilis and Milan Malfait
statOmics, Ghent University (https://statomics.github.io)
1 Cuckoo dataset
The common cuckoo does not build its own nest: it prefers to lay its eggs in another birds’ nest. It is known, since 1892, that the type of cuckoo bird eggs are different between different locations. In a study from 1940, it was shown that cuckoos return to the same nesting area each year, and that they always pick the same bird species to be a “foster parent” for their eggs.
Over the years, this has lead to the development of geographically determined subspecies of cuckoos. These subspecies have evolved in such a way that their eggs look as similar as possible as those of their foster parents.
The cuckoo dataset contains information on 120 Cuckoo eggs, obtained from randomly selected “foster” nests. For these eggs, researchers have measured the length (in mm) and established the type (species) of foster parent. The type column is coded as follows:
type=1: Meadow pipittype=2: Tree pipittype=3: Dunnocktype=4: European robintype=5: White wagtailtype=6: Eurasian wren
2 Goal
The researchers want totest if the type of foster parent has an effect on the average length of the cuckoo eggs.
In theory, they want to study this for all six species. Previously, we looked at a single pairwise comparison between the European robin and the Eurasian wren with a t-test. Here, we will analyse all types simultaneously with ANOVA.
Load the required libraries
library(tidyverse)
library(multcomp)2.1 Import the data
Cuckoo <- read_tsv("https://raw.githubusercontent.com/statOmics/PSLSData/main/Cuckoo.txt")
head(Cuckoo)3 Data tidying
It seems that the tpye column is a double rather than a factor. Let’s fix this:
Cuckoo <- Cuckoo %>%
mutate(type = as.factor(type)) %>%
mutate(type = recode(type,
"1" = "meadow",
"2" = "tree",
"3" = "dunnock",
"4" = "robin",
"5" = "wagtail",
"6" = "wren"
))4 Data exploration
How many birds do we have for each type?
Cuckoo %>%
count(type)Visualize the data
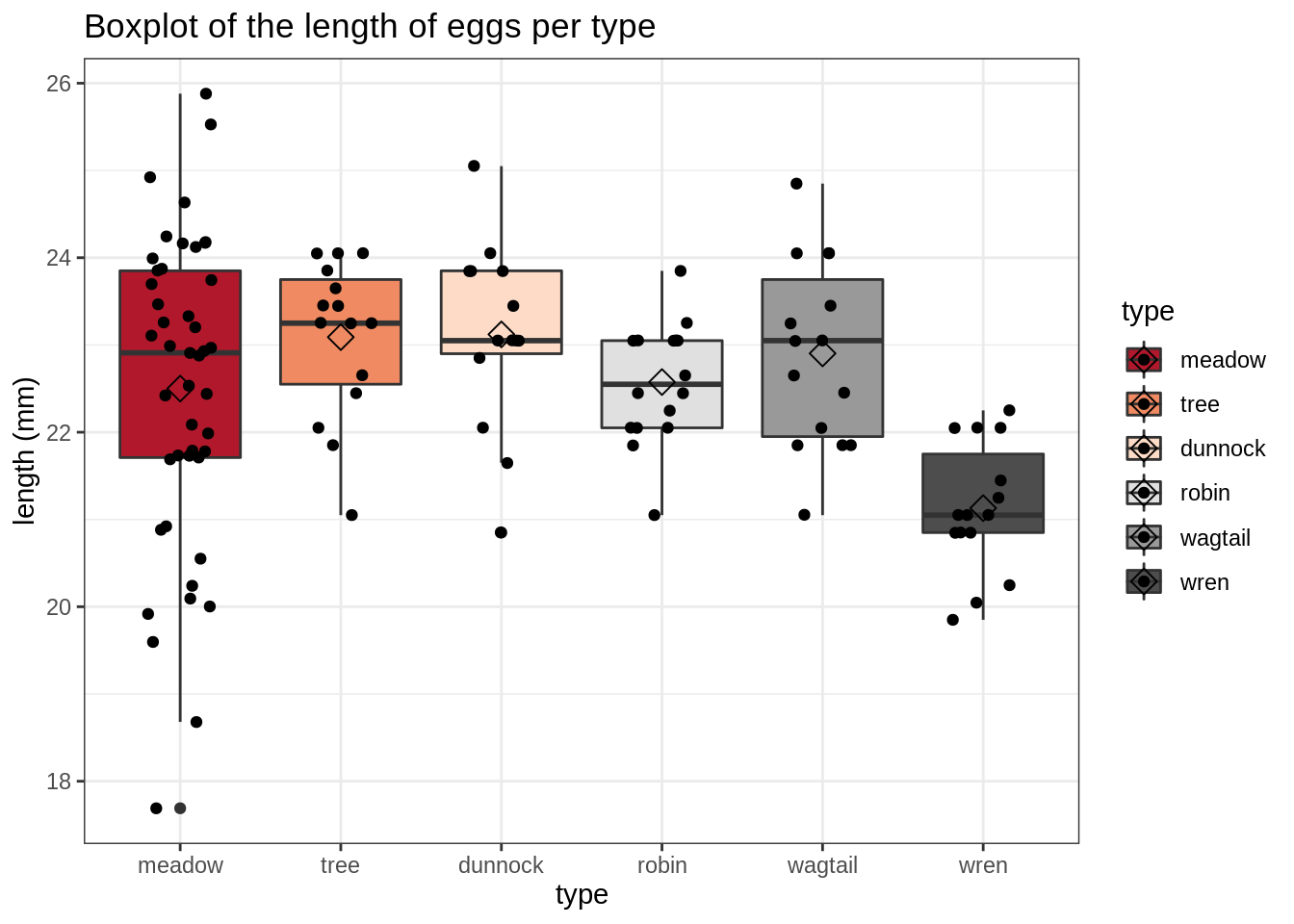
Cuckoo %>%
ggplot(aes(x = type, y = length, fill = type)) +
theme_bw() +
scale_fill_brewer(palette = "RdGy") +
geom_boxplot() +
geom_jitter(width = 0.2) +
ggtitle("Boxplot of the length of eggs per type") +
ylab("length (mm)") +
stat_summary(
fun = mean, geom = "point",
shape = 5, size = 3, color = "black"
)
5 ANOVA
To study if the observed differences in average egg length between the different foster bird types are significant, we can perform an ANOVA.
5.1 The model
We will fit the following linear model:
\[ E(Y_i) = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \beta_3 X_{i3} + \beta_4 X_{i4} + \beta_5 X_{i5} \]
where \(Y_i\) is the length of egg \(i\) and the coefficients \(beta_j\) corresond to the additional expected length of a cuckoo egg fostered by bird type \(j + 1\). By convention, the intercept is called \(\beta_0\) and it corresponds to the reference bird type, in this case bird type 1 (the Meadow pipit). The variables \(X_ij\) are dummy variables which take on the value 1 if egg \(i\) was fostered by bird type \(j + 1\) and are 0 otherwise. Note that in this case, eggs are always fostered by a single bird type, so only one of the X’s will be equal to 1.
For example, if egg \(i\) was fostered by the meadow pipit (type 1), all the \(X_{i1}, \dots, X_{i5}\) would be zero and we are left with:
\[E(Y_i | X_{i1} = \dots = X_{i5} = 0) = \beta_0\]
i.e. the intercept. If egg \(i\) was fostered by the European robin (type 4), we would have:
\[E(Y_i | X_{i3} = 1) = \beta_0 + \beta_3\]
So \(\beta_3\) can be interpreted as the change in average length of cuckoo eggs between the reference bird type (the meadow pipit) and the European robin. The coefficients can be negative or positive, so the change can be an increase or a decrease.
To further aid with intepretation, we can visualize the model design using the ExploreModelMatrix package:
ExploreModelMatrix::VisualizeDesign(Cuckoo, ~type)$plotlist[[1]]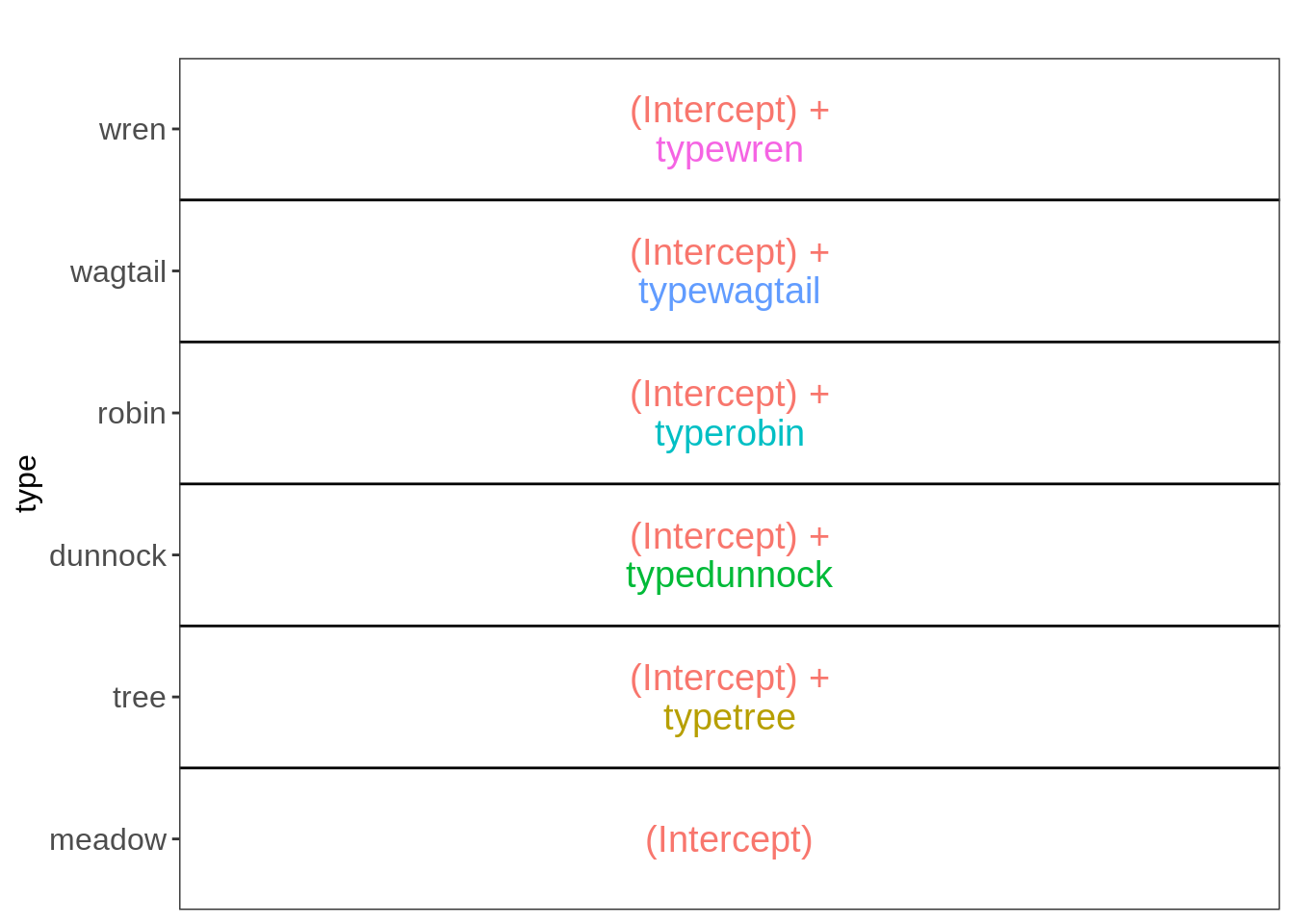
5.2 Formulate null and alternative hypothesis
The null hypothesis of ANOVA states that:
\(H0\): The mean egg length is equal between the different bird types.
In terms of the linear model:
\[ H_0:\ \beta_1 = \beta_2 = \beta_3 = \beta_4 = \beta_5 = 0 \]
The alternative hypothesis of ANOVA states that: \(HA\): The mean egg length for at least one bird type is different from the mean egg length in at least one other bird type.
\[ H_A:\ \beta_i \neq \beta_j \text{ for at least one } i \neq j \]
5.3 Parameter estimation
mod <- lm(length ~ type, Cuckoo)
summary(mod)##
## Call:
## lm(formula = length ~ type, data = Cuckoo)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.8100 -0.7212 0.1333 0.7775 3.3800
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.5000 0.1963 114.611 < 2e-16 ***
## typetree 0.5900 0.3926 1.503 0.135687
## typedunnock 0.6214 0.4030 1.542 0.125854
## typerobin 0.0750 0.3833 0.196 0.845225
## typewagtail 0.4033 0.3926 1.027 0.306475
## typewren -1.3700 0.3926 -3.489 0.000689 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.317 on 114 degrees of freedom
## Multiple R-squared: 0.1723, Adjusted R-squared: 0.136
## F-statistic: 4.747 on 5 and 114 DF, p-value: 0.0005621The output of the model suggests that there are indeed differences in the average length of cuckoo eggs between different foster parents. Note, however, that in the standard output of lm(), the p-values are not adjusted for multiple testing (a topic which we will touch upon later). In addition, this model only shows the differences between foster types 2-6 and the reference type (1), represented by the intercept.
The p-value of the F-test, given at the bottom of the summary, corresponds to a one-way ANOVA where the full model is compared to a reduced model containing only the intercept. Thus, it is testing the omnibus null hypothesis that all slope coefficients (\(\beta_1\) - \(\beta_5\)) are equal to 0.
5.4 Check assumptions
Before we may proceed with the analysis, we must make sure that all assumptions for ANOVA are met. ANOVA has three assumptions:
- The observations are independent of each other (in all groups)
- The data (length) must be normally distributed (in all groups)
- The variability within all groups is similar
The first assumption is met, as we may assume that there are no specific patterns of correlation between the randomly selected nests.
To check the normality assumption, we will use QQ plots.
plot(mod, which = 2)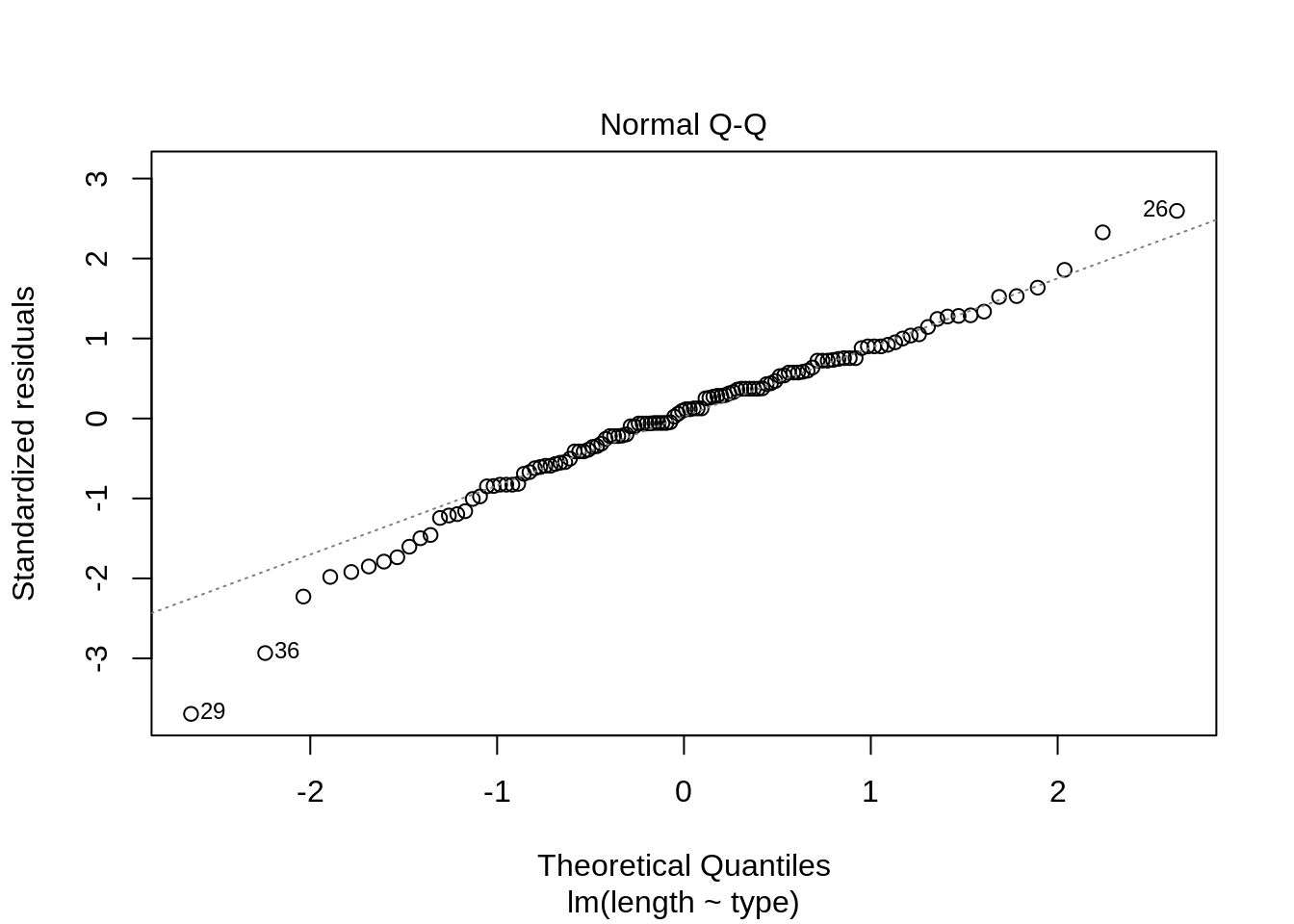
Cuckoo %>%
ggplot(aes(sample = length)) +
geom_qq() +
geom_qq_line() +
facet_grid(~type)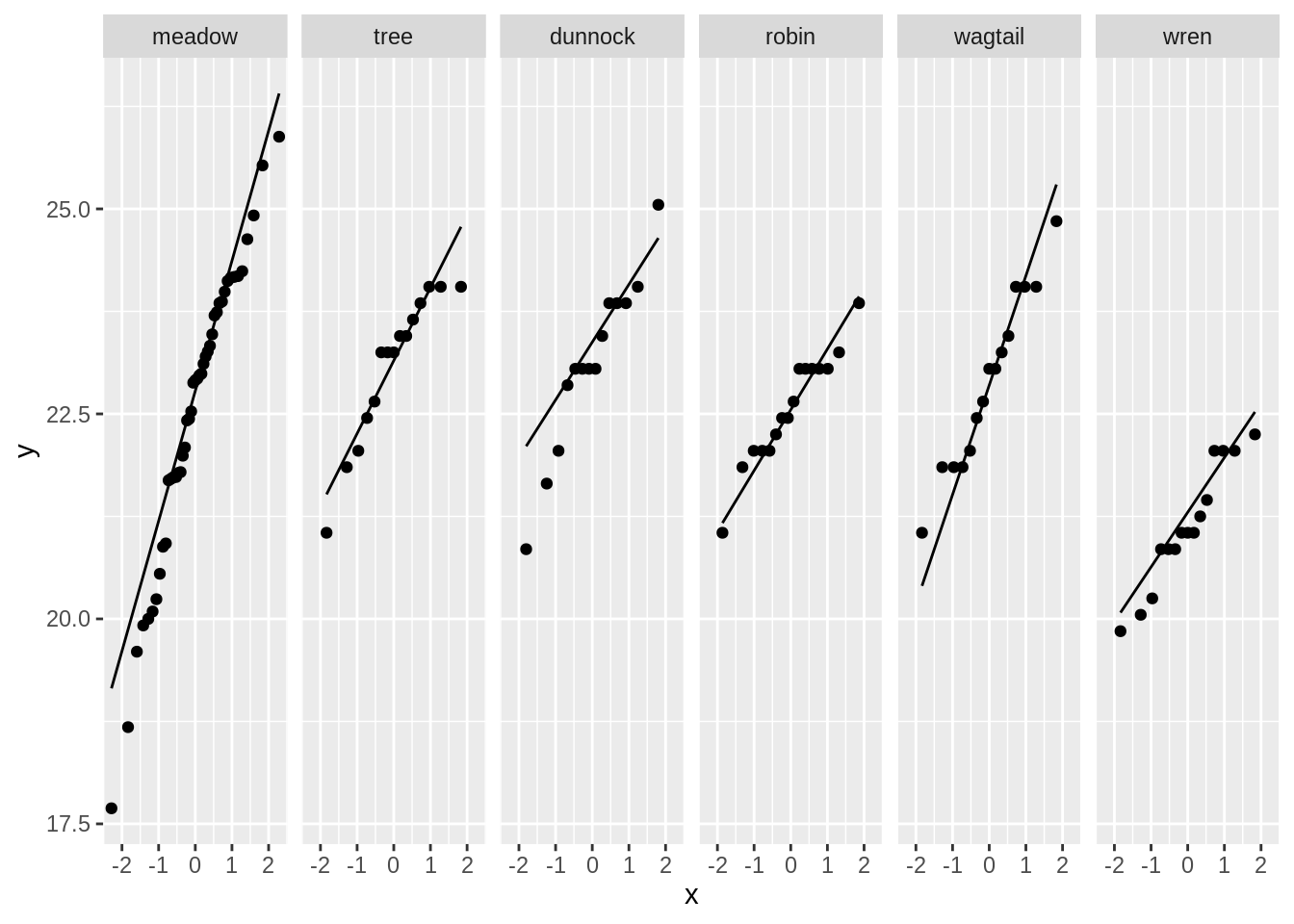
There seem to be no clear deviations from normality.
The third assumption of equal variances seems to be met based on the visualization with the boxplots (see above).
As such, we may proceed with the ANOVA analysis.
5.4.1 Simulate to train your skills in assessing assumptions
set.seed(1031)
sigma <- mod %>% sigma()
dataHlp <- Cuckoo
simModels <- list()
plotList <- list()
plotListQQ1 <- list()
par(mfrow = c(3, 3))
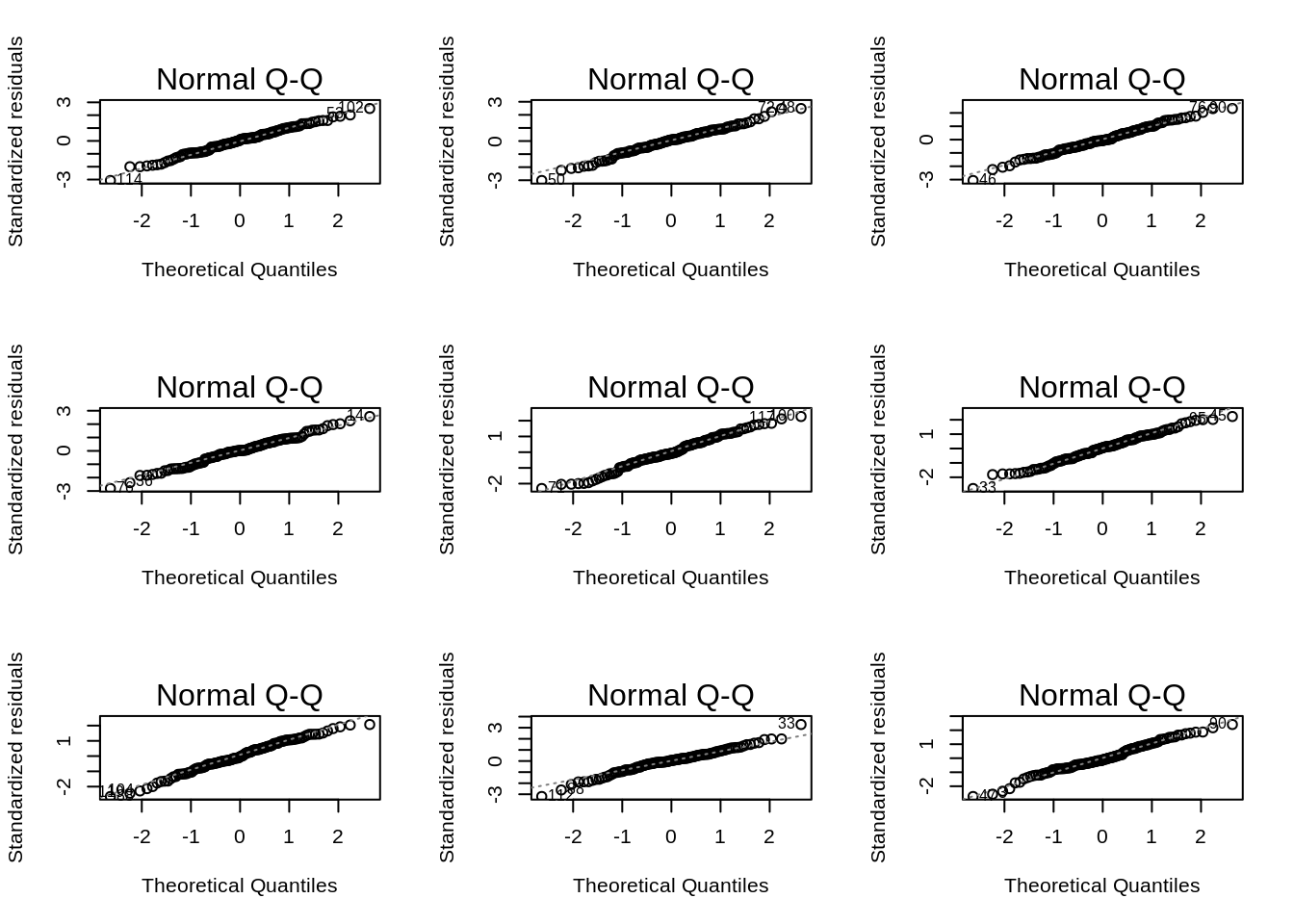
for (i in 1:9)
{
nobs <- Cuckoo %>% nrow()
dataHlp$ySim <- mod$fit + rnorm(nobs, sd = sigma)
simModels[[i]] <- lm(ySim ~ type, dataHlp)
plot(simModels[[i]], which = 2)
plotList[[i]] <- dataHlp %>%
ggplot(aes(type, ySim)) +
geom_boxplot(outlier.shape = NA) +
geom_jitter()
plotListQQ1[[i]] <- dataHlp %>%
filter(type == "meadow") %>%
ggplot(aes(sample = ySim)) +
geom_qq() +
geom_qq_line() +
xlab("QQ for meadow")
}
do.call(gridExtra::grid.arrange, plotList)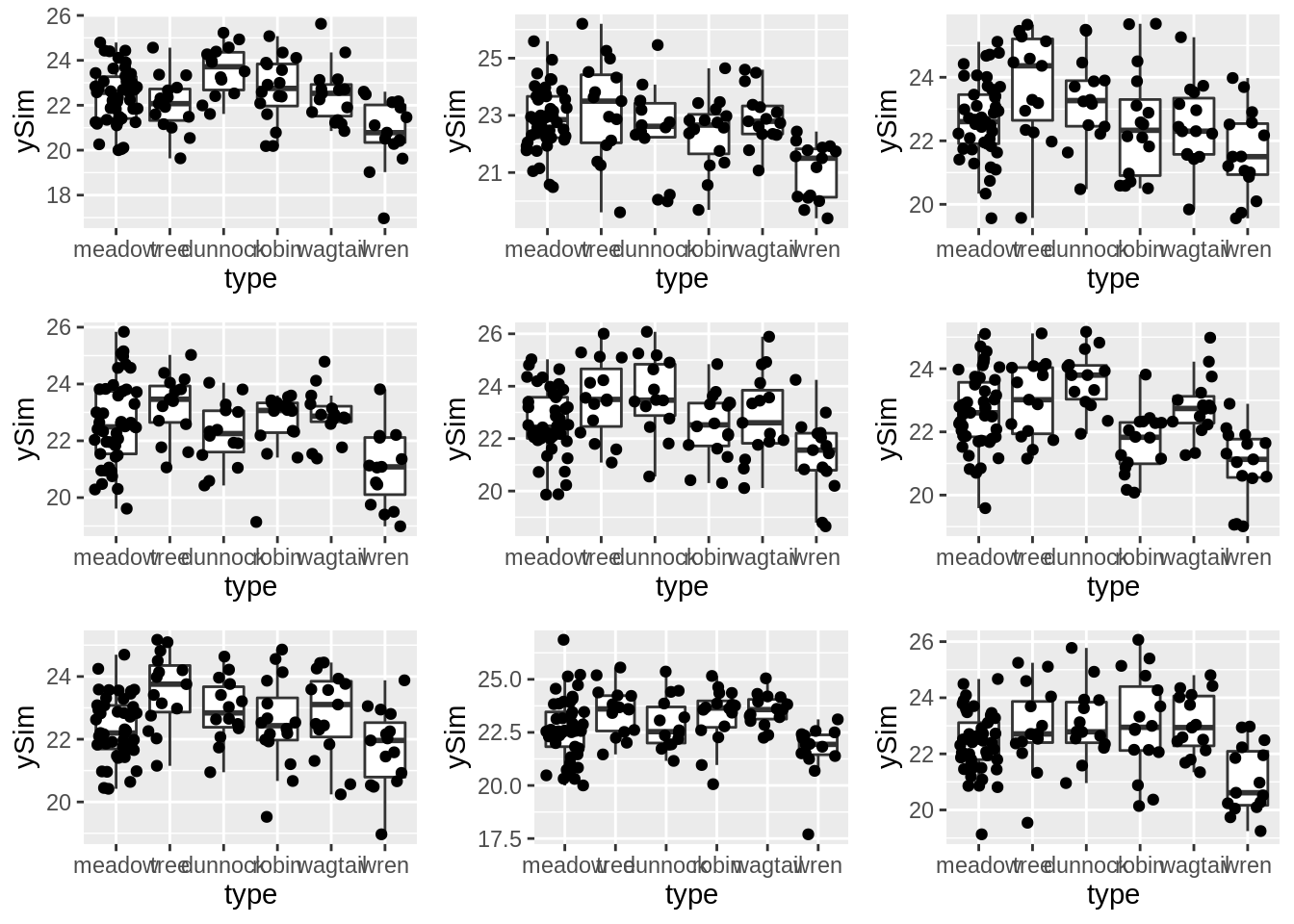
do.call(gridExtra::grid.arrange, plotListQQ1)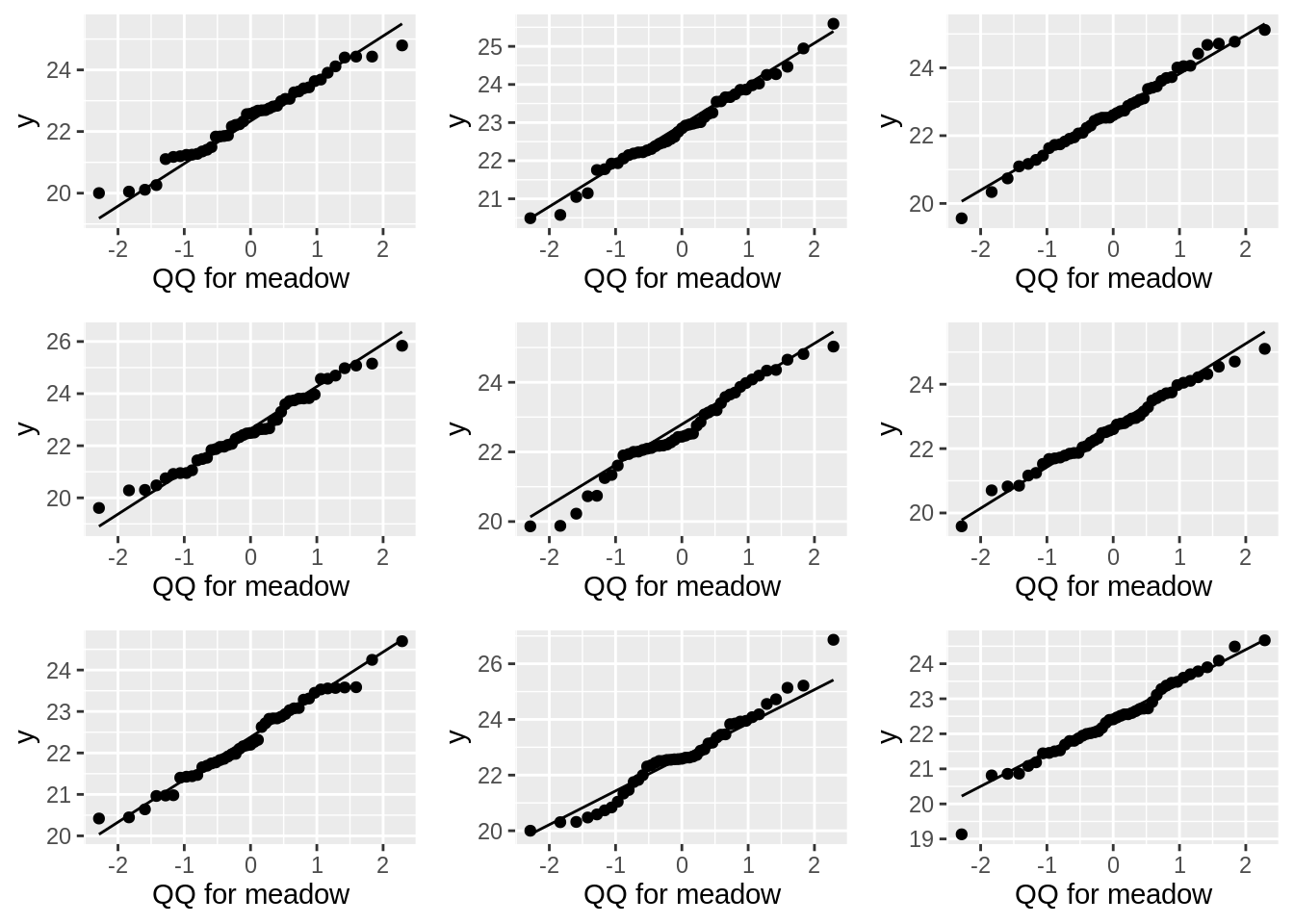
The most deviating QQ-plot of the residuals in the nine simulation runs:
par(mfrow = c(1, 1))
plot(simModels[[8]], which = 2)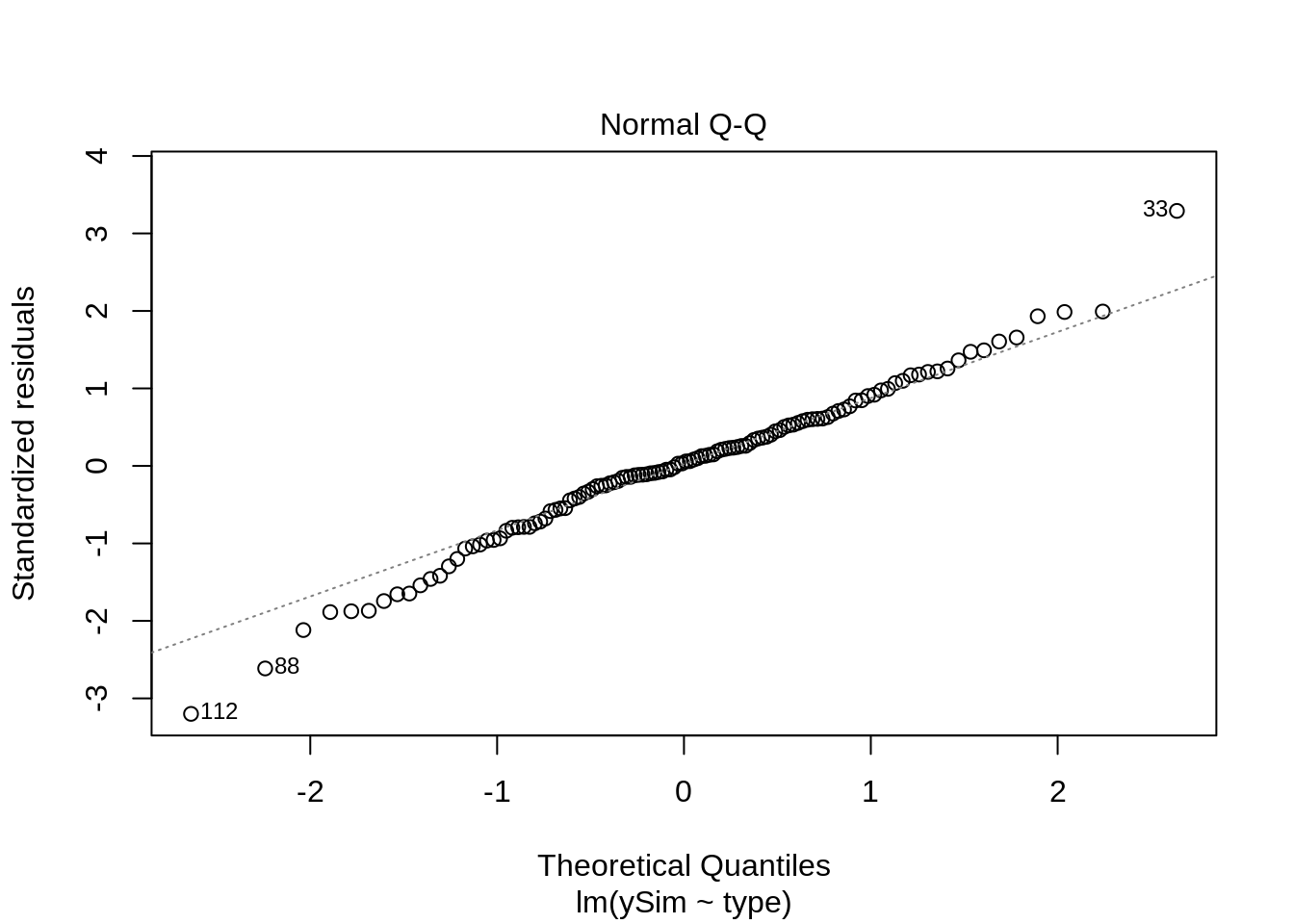
5.5 ANOVA model
We perform the ANOVA test using the results of the linear regression model. Essentially, we test the following null hypothesis:
\[ H_0:\ \beta_1 = \beta_2 = \beta_3 = \beta_4 = \beta_5 = 0 \]
with the alternative being that at least one of the parameters is different from 0.
anova(mod)The p-value of the ANOVA analysis is extremely significant (p-value < 0.001), so we reject the null hypothesis that the mean egg length is equal between the different bird types. We can say that the mean egg length is significantly different between at least two bird types on the 5% significance level.
Based on this analysis, we do not yet know between which particular bird types there is a significant difference. To study this, we will perform a Tukey post-hoc analysis.
5.6 Post-hoc analysis
We will perform a post-hoc analysis, to look at the difference in egg length between each pairwise comparison of bird types. Importantly, with this strategy, the p-values will be correctly adjusted for multiple testing.
The null hypothesis for each pairwise test is that there is no difference in the mean egg length between both bird types.
The alternative hypothesis for each pairwise test states that there is indeed a difference in the mean egg length between both bird types.
We will also calculate the confidence interval on the mean differences.
The post-hoc analysis is carried out using the glht() (“General Linear Hypotheses”) function from the multcomp package. We apply this to our linear model object mod and specify in the linfct= argument that we want to perform multiple comparisons (mcp), using Tukey’s method. We store the output of glht() and then display the results using the summary() function and calculating confidence intervals.
mcp <- glht(mod, linfct = mcp(type = "Tukey"))
summary(mcp)##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: lm(formula = length ~ type, data = Cuckoo)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## tree - meadow == 0 0.59000 0.39263 1.503 0.65686
## dunnock - meadow == 0 0.62143 0.40301 1.542 0.63147
## robin - meadow == 0 0.07500 0.38332 0.196 0.99996
## wagtail - meadow == 0 0.40333 0.39263 1.027 0.90518
## wren - meadow == 0 -1.37000 0.39263 -3.489 0.00847 **
## dunnock - tree == 0 0.03143 0.48939 0.064 1.00000
## robin - tree == 0 -0.51500 0.47330 -1.088 0.88202
## wagtail - tree == 0 -0.18667 0.48087 -0.388 0.99878
## wren - tree == 0 -1.96000 0.48087 -4.076 0.00114 **
## robin - dunnock == 0 -0.54643 0.48195 -1.134 0.86268
## wagtail - dunnock == 0 -0.21810 0.48939 -0.446 0.99764
## wren - dunnock == 0 -1.99143 0.48939 -4.069 0.00115 **
## wagtail - robin == 0 0.32833 0.47330 0.694 0.98170
## wren - robin == 0 -1.44500 0.47330 -3.053 0.03198 *
## wren - wagtail == 0 -1.77333 0.48087 -3.688 0.00433 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)confint(mcp)##
## Simultaneous Confidence Intervals
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: lm(formula = length ~ type, data = Cuckoo)
##
## Quantile = 2.8889
## 95% family-wise confidence level
##
##
## Linear Hypotheses:
## Estimate lwr upr
## tree - meadow == 0 0.59000 -0.54429 1.72429
## dunnock - meadow == 0 0.62143 -0.54285 1.78571
## robin - meadow == 0 0.07500 -1.03239 1.18239
## wagtail - meadow == 0 0.40333 -0.73096 1.53763
## wren - meadow == 0 -1.37000 -2.50429 -0.23571
## dunnock - tree == 0 0.03143 -1.38238 1.44524
## robin - tree == 0 -0.51500 -1.88234 0.85234
## wagtail - tree == 0 -0.18667 -1.57589 1.20255
## wren - tree == 0 -1.96000 -3.34922 -0.57078
## robin - dunnock == 0 -0.54643 -1.93875 0.84589
## wagtail - dunnock == 0 -0.21810 -1.63190 1.19571
## wren - dunnock == 0 -1.99143 -3.40524 -0.57762
## wagtail - robin == 0 0.32833 -1.03901 1.69567
## wren - robin == 0 -1.44500 -2.81234 -0.07766
## wren - wagtail == 0 -1.77333 -3.16255 -0.38411We can also visualize the confidence interval by calling plot() on the mcp object:
plot(mcp)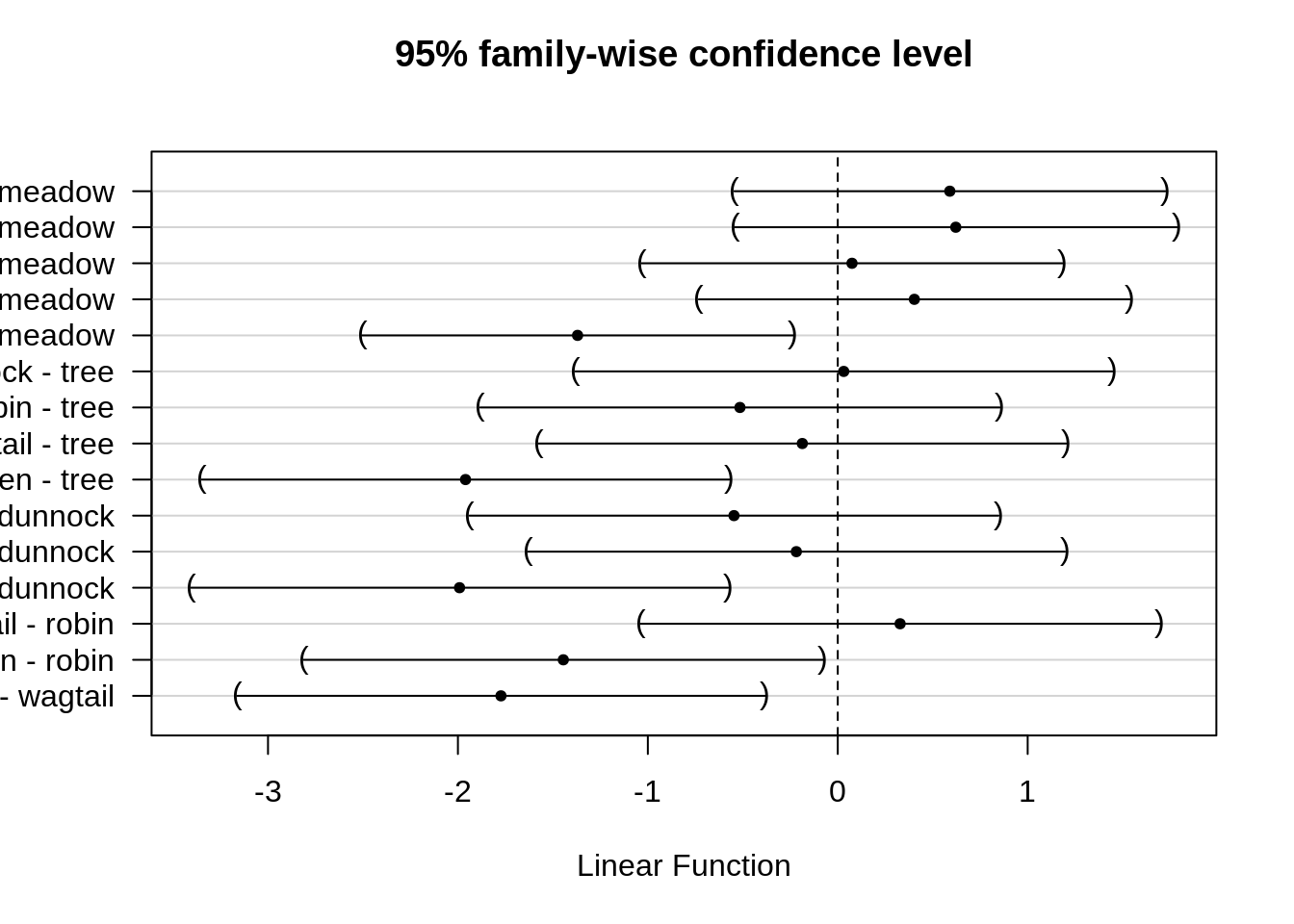
5.7 Conclusion
The association between the mean length of a cuckoo’s egg and the foster bird species is extremely significant (p << 0.001).
The mean length of cuckoo’s eggs in nests of the Eurasian wren are smaller as compared to those from all other bird species in the study:
- the meadow pipit (adjusted p-value = 0.009, mean difference = -1.4mm, 95% CI [-2.5, -0.2])
- the tree pipit (adjusted p-value = 0.001, mean difference = -2mm, 95% CI [-3.3, -0.6])
- the dunnock (adjusted p-value = 0.001, mean difference = -2mm, 95% CI [-3.4, -0.6])
- the European robin (adjusted p-value = 0.03, mean difference = -1.4mm, 95% CI [-2.8, -0.1])
- the white wagtail (adjusted p-value = 0.004, mean difference = -1.8mm, 95% CI [-3.2, -0.4])
There is no evidence taht the mean length of the cuckoo bird’s eggs for all other pairwise comparisons between foster bird species are significantly different at the 5% level.