Theory

Introduction

• Methods based on distances are typically very fast compared to model-based methods that will be discussed later
  • Generating a distance matrix
  • Constructing a tree by neighbour joining
  • Generating a network of 'clustered' sequences

Generating a distance matrix

• Given a multiple sequence alignment, there are several models of DNA evolution that have been proposed e.g.
  • JC69
  • HKY85
  • TN93
  • GTR
• See Wikipedia for a nice description of these

Distance calculations

• An estimate of the distance between pairs of sequences can be obtained using a closed expression for several of these models

The Tamura-Nei (1993) model

• Unequal base frequencies
• Different rates of A-G and C-T transitions- The transversion rate can be different from the transition rate

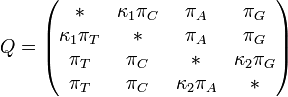
Source: Wikipedia

Neighbour joining

• Given a distance matrix, the neighbour joining algorithm builds a tree
  • Identify the closest neighbours using information from the distance matrix
  • Join neighbours
  • Calculate distance of taxa in the pair to new node
  • Calculate distance of taxa outside the pair to the node
  • Replace joined neighbours with new node and repeat

NJ algorithm

Measuring error

• Neighbour joining produces a single tree, with no assessment of goodness-of-fit, or any idea of confidence in the tree
• A common approach to obtain a confidence set of trees is to bootstrap the sequences

Bootstrapping

• Classical statistical inference is based on the concept of hypothetical repetitions
• Bootstrapping involves random resampling of the data with replacement
• For sequence data, by generating new datasets from the old one, by resampling the columns of the sequence alignment

Clustering

• While a tree may capture 'deep' evolutionary relationships